Introduction
A few years ago, I wrote a lengthy article about birdsmouth spars' math. Some time after that, someone (1) sent me an interesting link to the Lee Valley tools Website (2), showing their router cutting bits for birdsmouths. Of particular interest were the modified 6 and 8-sided birdsmouths these bits could make:
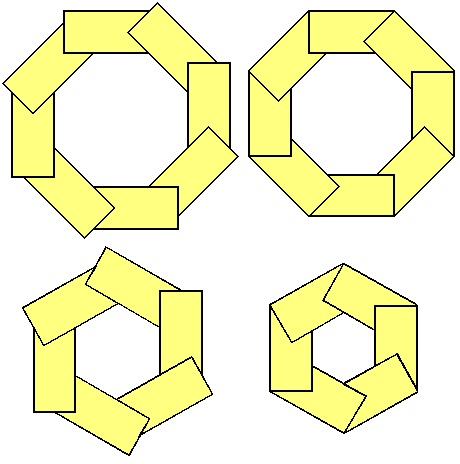
|
Fig.1- Left: original birdsmouth shape. Right: modified version |
As you can see, these modified versions are regular polygons with a cleaner outside surface than the original birdsmouths. There are two distinct advantages to that. First, the diameter calculations are much simpler. Second, the perfect polygon shape produced would be quite usable as is, and woodturning on a lathe could be avoided.
Now, I have no financial ties to Lee Valley (3), and the staves for such a birdsmouth spar could likely be cut on a table saw, if you don't have a router table.
Stave details
The way the V-groove is cut on the edge of the staves explain why the diameter formula is simpler. Let's look at the 8-sided spar.
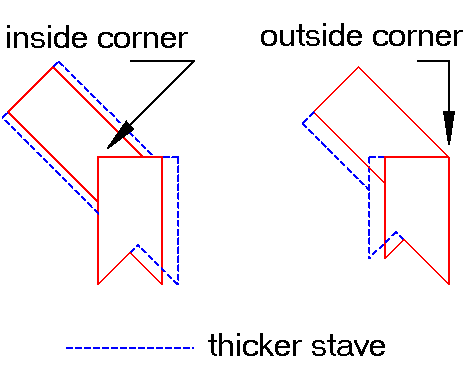
|
Fig.2- Effect of stave thickness. Left: original birdsmouth stave. Right: modified stave |
On the original version, that V-groove is cut at at half the thickness: it is centered. The inside corner of the next stave is fitted there. So, if you use a thicker stave, part of that extra thickness will be added to the inside, the other part to the outside, producing a larger overall diameter. The formula is thus dependent on both the width and the thickness of the staves.
On the modified version, the outside corner is flush with the outside tip of the “V” groove. If you use a thicker stave, all the extra thickness is added to the inside. The stave's thickness no longer has an effect on the overall diameter. The stave's width alone sets the size. And since the outside shape is a simple regular polygon, the formula for size becomes quite simple, compared to the original birdsmouth.
Size calculations
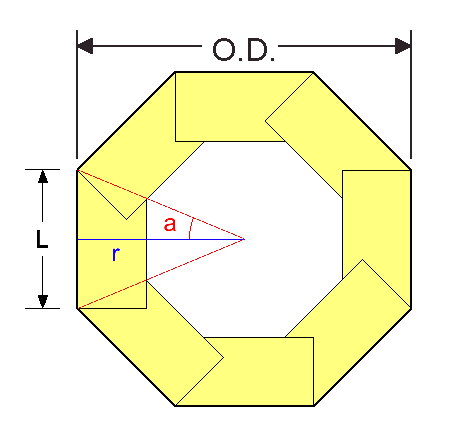
|
Fig.3- Determining size. |
The formula for calculating the radius of a regular polygon is:
Where:
r
L
N
cot
|
is the radius
is the outside width of the staves
is the number of sides
is the cotangent of the angle a in degrees |
The angle value of a, shown in Figure 3, is 180 degrees divided by the number of sides N. For an 8-sided polygon, that angle value is 22.5 degrees. For a 6-sided polygon, the angle value is 30 degrees. The outside diameter ( O.D. ) being twice the radius, the formula we are looking for is:
For an 8-sided polygon, the formula can also be expressed in this way:
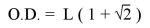
|
8-sided |
Or, in its most simple numeric form:
For a 6-sided polygon, the formula would be:
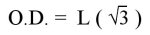
|
6-sided |
Likewise, in its most simple numeric form:
Simple, isn't it? Compare that to the formula for the original birdsmouth shape:
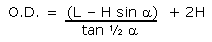
|
Fig.4- Size formula for the original birdsmouth. H is the stave thickness. |
Less Waste, Less Work
Given the resulting shape of this modified version, it becomes quite tempting to use it as is, without going to the trouble of setting a special, long lathe. When I build my first sailboat, this is probably what I'll do, as I have no lathe and no training on using one.
But even if you do use a lathe, you may notice that, once rounded, there is less waste with these modified birdsmouth spars. For example, using staves one-inch wide by half-inch thick, woodturning the resulting spar will remove about 10.5% wood on a conventional birdsmouth. With the modified version, you would remove only about 7.9% wood. A good improvement. That means less work and also a slightly stronger spar.
Any Drawbacks?
There is one small drawback: if you want a perfect fit, you will need to cut the V-grooves on your staves perfectly. On the original birdsmouth, if you cut your V-groove a bit off center, it won't make a huge difference on how the outside looks, since the outside corners will protrude anyway. Only the overall diameter is affected notably.
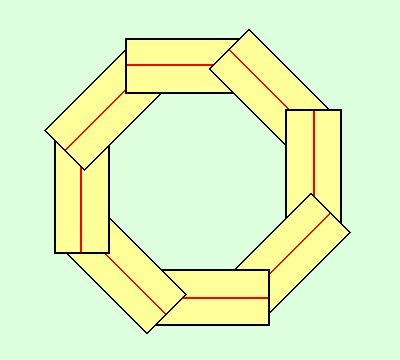
|
Fig.5- Imperfect V-groove cutting, original birdsmouth. The red lines are the center of the staves. The overall diameter is affected, but the spar looks just the same. |
On the modified birdsmouth, the outside leg of the V-groove has to be the exact width of the stave thickness, otherwise one end of the stave or the other will protrude. If you intend to round the spar on a lathe, that's not really a problem. If you want to avoid using a lathe, however, you will have to be real precise to achieve a good fit. Otherwise some trimming will be in order.
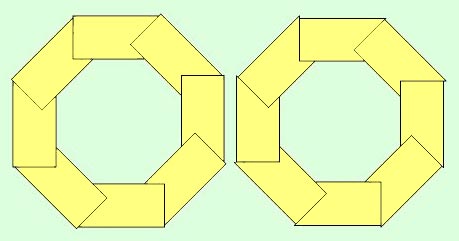
|
Fig.6- Imperfect V-groove cutting, modified birdsmouth. Left: too shallow, right: too deep. |
If your V-grooves are not cut at quite the right angle, both types will have some gaps where the staves join.
Final Word
That pretty much covers what I had to say on the subject. I hope you find these modified birdsmouth spars worthy of interest.
NOTES
- I don't remember who sent me the information: my apologies to the person involved.
- Here is the link to the Lee Valley Website.
Although they offer cutters for producing 6, 8, 12 and 16-sided spars, only the 6 and 8-sided spars offer the unique properties discussed in this article.
- All the math and illustrations in this article were done by me, so there is no unauthorized material copied from the Lee Valley Website.
|

