Merrell
Watercraft
Private
Postings
Micro Page
Bill
Sampson's
Book Reviews
Chebacco
News
boatdesign.com's
Nautical and Marine
Resource List
Craig O'Donnell's
Cheap Pages
Tomboy
|
Slogging
to Windward
by Chuck Merrell
sloggingtowindward@hotmail.com
February 2001
DESIGN ANALYSIS RATIOS
Part 2 - "Interpretation"
DESIGN ANALYSIS RATIOS
Part 2 - "Interpretation"
(be sure to read Part 1)
Like many others, I've been watching the current Vendee Globe
"single-handed, round the world non-stop" sailboat race using Virtual Spectator
with great interest. Today, January 31, 2001 is the 84th day of the race, and with only
about 2700 miles to go, it looks like the winner will set a new course record of fewer
than 100 days. At the moment, veteran sailor, Michel Desjoyeaux holds first place sailing
PRB. However, the real story of this Vendee Globe is in second place in the person of 24
year-old, 5'2", and 110-pound dynamo, Ellen MacArthur from Derby, England. Ellen,
skipper of Kingfisher has picked up 600 miles on Desjoyeaux and briefly was in the lead
two days ago. It looks like it's turning into a drag race to the finish line between these
two leaders. I'm hoping that Ellen will prevail and become the first woman to win the
Vendee Globe. GO ELLEN! For more information on the race, Ellen and direct daily (Real)
audio updates from Ellen herself, click:
https://www.kingfisherchallenges.com/
Design Analysis Ratios
Many analytical formulas exist which are supposed to shed light on various aspects of
boat design. However, with the exception of the Prismatic Coefficient, at this time
we’ll deal only with those which can be calculated and interpreted by anybody using
the simple data normally included with the publication of a particular design. Moreover,
I’m going to ignore those that yield limited information, one of which is the
Ballast/Displacement ratio. The B/D is supposed to indicate stiffness of a particular
hull, but it really doesn’t. All it shows is whether the ballast related to the
overall displacement of the boat is or is not within the average design envelope-or not.
Terms used in the formulas

Speed to Length Ratio
For some reason, the first ratio we usually encounter is the S/L, which is written:
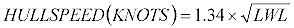
This is the theoretical hull speed for a displacement hull. Most sailboats are
classified as displacement hulls. It is a function of the length of the wave created by
the boat as it moves through the water. Wave speed is a function of wavelength. The longer
wavelength is faster. Longer boats make longer waves. Since longer waves are faster, boats
that make longer waves are faster. The 1.34 factor used in the equation represents the
maximum speed that a displacement hull can be pushed or pulled through the water BEFORE
the force required to make the hull go faster becomes inordinately high. In fact, 1.34 is
what some call the breakaway point where the stern of the hull drops into the hole made by
the stern wave, and the bow tries to climb the bow wave and attempts to surf as a power
boat does. In the case of a displacement hull, the shape and strength of the stern
sections of the hull largely prevent surfing under normal conditions, however racing boats
with strong aft sections often do surf, but the forces applied to the hull are also
relatively massive.
The Prismatic Coefficient
The next Design Analysis Formula usually encountered is the so-called Prismatic
Coefficient. I say "so-called" because I’ve always felt that the name of
this formula is confusing and should be renamed the Prismatic Percentage. I include the Cp
(symbol for the Prismatic Coefficient) in this discussion because while the information
published with a design usually is not enough to calculate this number, the Cp is often
included in the list of specifications.
While not particularly important knowledge for the casual reader, the Prismatic
Coefficient is the most important formula for the sailboat designer. The Cp compares the
volume of the hull to that of a prism having the same shape for the full length of the
waterline as the largest actual section. The coefficient reflects the
"percentage" of the original prism that remains after the hull is carved out.
The formula for the Cp is:
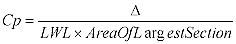
Perhaps the following drawing will be of help in visualizing:
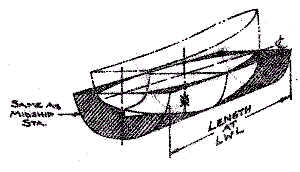
In other words, the number generated and called the Cp show the relative
"fineness" or "fullness" of the ends of the hull under consideration.
In sailboats, fineness or fullness indicates a boat that is either sleek and weatherly or
tubby and not efficiently close winded. Sailboat hulls with a fine entry go to weather
better, but are slower at the top end than hulls that are fuller. In fact, the resultant
prismatic index bears closely on the potential speed to length ratio (see above) of a
specific hull. For example, all things being equal, a hull with a Cp of .52 would have a
S/L ratio of 1.0. A hull with a 36 ft. waterline would have a maximum theoretical speed of
6 Knots. However, a hull with a 36 ft. LWL and a Cp of .62 would have a maximum
theoretical speed of 7.8 knots, about a 20% increase. However there are other factors to
be considered, and depending on what the designer desires from a design, a tubbier hull
that is potentially faster may not be what is required for the job at hand. Those
considerations are really up to the designer, though, and that’s why the Prismatic
coefficient isn’t of much help to the casual reader. Not only that, but the person
reading the design data also must know (like have a chart in his head) the Speed/Length
ratio relationship as applied to the Cp numbers in order to interpret the number relative
to a given design.
For the designer, however, by transposing the Cp formula, the designer can
mathematically design a hull to very precise perimeters-or in the case of modern hull line
generation programs, can vary the prismatic and simultaneously physically visualize (on
the screen) the effect of changed hull shape and speed potential.
Displacement to Length Ratio (D/L)
Fundamentally, the D/L formula produces a non-linear index number ranging from about 40
for Ultra Light Displacement Vessels to over 500 for the very heaviest boats. What the
ratio is supposed to indicate is how heavy a boat is relative to its waterline length, and
by interpretation how comfortable (or uncomfortable) it might be in a seaway, and how a
particular boat with a particular number may compare with a similar boat with similar
index. The inference is if you have experience with a boat having a D/L of 250, then you
should know about what any boat with a similar D/L might feel and perform like, but this
is only true if the length of the LWL’s of both hulls are the same. The flaw in this
formula, confusing particularly for newcomers to the idea is that two boats completely
different in length can have comparable D/L indices, but will feel and perform at opposite
ends of the spectrum. For example, take a 20 ft. keel boat with a D/L of 50, and
you’ll have a boat that’ll jump all over the place and be totally uncomfortable
and unacceptable in any body of water other than a mill pond. On the other hand, you can
have a 60 ft. boat with a D/L of 50 and the motion and pitching moment not only may be
very acceptable even in rough weather, but overall quite comfortable in general. A good
example of this is the boats currently used in the Vendee Globe. I don’t have any
stats for Vendee boats (Finot and the other designers are pretty secretive about those
numbers), but I’m sure that based on what I see and what the skippers complain about
in terms of comfort, I’d say that the D/L’s are well below 100, possibly even
less than 50.
So, in order to be useful to the individual, he/she needs to have a reasonable amount
of hands on experience (the more the better) with many different sailboats. Then by
relating the D/L’s of those boats to the LWL and D/L number of new designs you can
get a good idea of what that new design will be "like".
Regardless of these discrepancies and inconsistencies, though, the D/L is a good index
albeit non-linear. The best way to get am understanding of how it all relates is to run
the formula for every boat you’ve ever sailed and plot it both on a spread sheet and
on an X-Y graph/chart then when you see a D/L index number for a new hull and know what
the LWL is, your mind, in concert with your charts and past experience, will fill in the
blanks and you’ll have a "knowing" about that new boat under scrutiny. The
D/L Formula is:
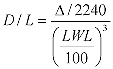
Sail Area Displacement Ratio
(Power to Weight Ratio) SA/D
This formula simply supplies a (linear) number between 8.0 and 25.0, which expresses
the amount of power of a boat’s working sail plan and relates it to the displacement
of the boat. The SA/D formula is:
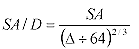
The SA/D is generally thought of in context with the D/L. Normal cruising sailboats
have a SA/D index ranging between 15 and 16. In general, the higher the index becomes, the
more disproportionate the sail plan looks in relation to the hull. Too large a sail area
can make the overall design look grotesque and out of proportion, and be hard to handle in
operation. Like everything else, there are exceptions to the rule and even as applied to
the visual look of a boat.
For example, America’s cup boats often have a SA/D of 25+. The reason 12 meter
boats get away with these huge rigs is because of the narrow range of conditions these
boats race in. In the last Cup in the Harukki Gulf in New Zealand, race conditions ranged
from flat calm to about 20 knots. On race days when winds started pushing speeds of 20 to
25 knots, the races were postponed or cancelled by mutual agreement for no reason other
than to protect the boats from harm (not nice to break a mast costing a million
dollars-the Italian boat Prada did lose one, and America First almost did). America’s
cup boats do not have reefing gear-what blows is what you gotta sail in.
Anyway, getting back to earth, a 35 ft. LOA cruising sloop designed for use by us
normal mortals might have the following ratios. D/L: 270, SA/D: 15.7, Cp: .60, S/L: 7.1
kts.
Based on that what might you have? Try a conservative coastal and offshore cruiser with
moderate overhangs designed in the late 60’s by Sparkman and Stevens capable of good
performance, fairly fast (as boats that size go), reasonable comfort in a seaway and
acceptable motion even in heavy weather. In other words, you’d have a boat that
resembled something designed with the old CCA rule in mind.
In reading back over this, I see the column has gotten longer that it should. Drat! I
wanted to discuss Ted Brewer’s Motion/Comfort Ratio, the Water Plane Loading Ratio,
and the Capsize Screening formula, but those will have to wait for a future column. In the
meantime, now that you understand all the above, and how to interpret the calculations and
INTERPOLATE the numbers (weighted by personal experience) between the various ratios,
especially the D/L and SA/D, you can break out your scientific calculators and try out
some number crunching. OR, you can click on the following link, which will take you to
"Carl’s Sailing Calculator". Plug in the numbers for any design you want to
find out about and all the answers will be done for you automatically! Below is a screen
shot of the calculations for TestBench, the design example I used in last month’s
column.
https://www.image-ination.com/sailcalc.html
|
![]()